Lors de l’article précédent, deux modèles très simples pour répondre à la problématique d’attribution des parcours client ont été évoqués. Il en existe d’autres qui leur ressemblent beaucoup, mais ici nous allons évoquer un modèle qui nécessite des connaissances mathématiques un peu plus solides.
Présentation du modèle
Pour la création de ce modèle, c’est la théorie probabiliste des chaînes de Markov qui va être utilisée. En effet, les chaînes de Markov permettent de mettre en avant la probabilité de passer d’un état à un état suivant dans un chemin. Dans le cas de l’application de l’attribution, nous avons autant d’états que de canaux, auxquels s’ajoutent les états de début et de fin : début, conversion, non-conversion. Les différents parcours client ressemblent par exemple à ceci :
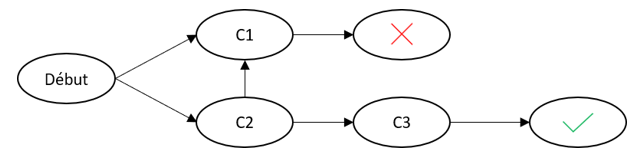
Sur cet exemple, le parcours C2 puis C3 finit sur une conversion, alors que le parcours C2 puis C1 n’apporte pas cela. Ici, il est par exemple très clair que le canal 1 n’apporte jamais d’achat, c’est donc inutile de continuer à payer pour lui.
Répartition des poids
Une fois que le graphe représentant les parcours client est construit, il faut connaître l’impact de chaque canal, pour ne pas reproduire un modèle trop simpliste comme le modèle linéaire présenté succinctement dans le dernier article où tous les canaux ont le même poids. Ici, pour calculer les poids correspondant aux canaux, il faut, un à un, les supprimer du graphe et observer l’impact sur la probabilité finale de conversion. C’est en fonction de cet impact qu’un poids pourra être déterminé.
Cet exemple est très simpliste néanmoins le principe reste le même sur des graphes bien plus imposants, où il est donc possible de voir quels sont les parcours qui ont peu de chances de mener vers une conversion et quels sont ceux en revanche qui y mène presqu’à coup sûr. Dès lors que cette information est connue, il va être possible d’adapter le parcours en fonction du type de client et donc d’améliorer les conversions et le réachat en dépensant moins qu’auparavant et de façon plus ciblée.
Limite des chaînes de Markov
La limite des chaînes de Markov dans ce cas présent est que la probabilité de succès d’un état ne dépend que du précédent, et pas de ceux d’avant. Il existe une solution à ce problème, qui est celle d’utiliser des chaînes de Markov d’ordre supérieurs, qui donc vont prendre en compte les x derniers états. Le principe reste le même tout en étant plus proche de la réalité.
Naïa Lollichon
Data Analyst